残阳似血的博客

声明：这篇文章中涉及的游戏来自@陈荣峰ayuLemon的创意，文章的主要目的还是研究这个游戏其中的算法，我所写的网页版的游戏版本也仅仅是为了验证算法的正确性。说明这个是防止大家误认游戏乃我的原创。本来原作者要求我不能在他的算法出来之前发出此文，我百思不得其解。我认为这个没有先后顺序，思前想后，还是发出来了。仅讨论之用。

事情的起因是这样的，在我又度过了一个不眠之夜、正打算睡觉之时，看到@python4cn 转发了一个同学的微博，原文是这样的：

@陈荣峰ayuLemon：用python做了个小游戏，这是5*5方格。每点击上面的方格一次，就改变周围四个方格和被点击方格的颜色，对于任意n*n方格，可否通过若干次点击使方格的颜色与最初完全相反？？（3*3和4*4的都很容易~~这个5*5的似乎有困难） 大家帮忙想一想，证明行或者不行，哪些行，哪些不行~~

本来已经很困的我看到这个，又勾起了我的好奇。于是拿起纸笔，开始演算。当然首先从2×2开始，一直到4×4，确实没有什么困难。到5×5，算了很久才算出一个结果。

在分析这个问题之前，如果你想试玩，我做了一个网页版的，地址在这里。

从直观印象来说，对于四个角上的方块，点击了以后，会触发包括自身的三个方块；四个边上非角的方块，点击可以触发4个方块；而中间的方块可以触发5个。

我们先作一个假设，其中每一个方块最多只需要点击一次就可以完成这个任务。为什么作这个假设呢？因为一个方块它点偶数次，对自己是没有任何影响的，因为又回到原状态（如黑=>白=>黑）；如果点击奇数次，相当于只点击一次。同时，假设这个方块的点击对周围某个方块Ki造成了影响，这个方块Ki的状态经过了一系列的变化s1=>s2=>...=>sj（实际上也是黑白交错的过程），源方块的偶数次点击对这个方块的的状态并不会有影响；同样的奇数次个数相当于只点击一次。

在此假设上我们了解，任何方块最多一次点击就能解决问题，前提如果有解决方案的话。

但是之前的结果会让人越想越糟。但是相信大家都玩过扫雷，通过已经揭开的方块，我们可以依次推断是否有雷。同样的这个问题我们也可以这么解决。

我们来看对于某个方块，假设点击过，我们记它的值为1；否则为0。每个方块自身以及周围的方块，可能有3块、4块、5块，那么何时这个方块会反转呢？那就是几个方块的值的和为奇数。很简单不是？

现在，我们用一个矩阵（二维数组）来表示这n×n的方块。用(i, j)表示第i行j列的方块（i，j都是从0到n-1）。对于(0, 0)即左上角的方块，如果(0, 0)，(0, 1)，(1, 0)这三个的值和为奇数，表明(0, 0)方块必定会反转。

于是，我们经历这样一个过程，从左上角的方块开始，由于它的值不知是0或者1，于是我们假设为1，即反转自身。接着看(0, 1)和(1, 0)，这两个值必须同为1或者0。原因很简单，因为不相同，(0, 0)的周围值的和就不为奇数。假设它们的值都为1。以此类推，我们就像四周扩散，使用猜测或者准确的判断。如果发现最后的结果不对，我们就再回溯到之前某个点，比如说回溯到(0, 1)和(1, 0)的时候，当时假设他们同为1，现在假设同为0。然后依次类推。

推理很简单，可做起来就不那么容易了，很常见的是做到最后发现不对再回溯，真是让人恼火的事儿，看起来还真是碰运气啊。

不过，这种事，我们自然可以用程序来解决。由于我们的目标是求出一条路径即可，不需要求出所有的路径（当然可以求，不过费不费时间就不得知了）。下面给出我早上写的代码，采用的回溯法。我是用Python写的，还是那句话，为什么用Python，因为它方便（至于很多人拿Python命令行做计算器也就可以理解了）。不过，由于一大早，没睡觉的缘故，如果代码糟糕，希望大家理解。另外，有什么问题，欢迎大家提出。

我们从左上角开始，逐行扫描。首先，我们先定义一个列表，它专门用来做栈存放猜测的列表，到了某个方块，没法推断，就猜测是0，同时把这个方块压入这个栈中。然后接着运行，到最后如果不符合条件，就从栈顶取出方块，置为1继续运行。

那么，对于一个方块，我们何时能确定它的值呢？由于一个方块上下左右可能都有方块，但是它的值只能准确通过上面的方块（如果有的话，上面的方块的上左右以及自身值都已经确定）得出。而左边的方块由于下面的值未定，所以不能通过其确定。右边和下边的就更别说了（还没运行到呢）。遇到不确定的方块，就猜测0，然后把它的坐标值压入栈。

下面是一大段代码。

#!/usr/bin/env python
#coding=utf-8

class Matrix(object):
    '''矩阵，用来表示n*n方格'''
    def __init__(self, n):
        self.n = n
        self._matrix = [[-1 for j in range(n)] for i in range(n)]
        # 初始化

        self._guess_list = [] # 猜测列表

    def display(self):
        # 打印矩阵
        for i in range(self.n):
            output = ''
            for j in range(self.n):
                output += str(self._matrix[i][j]) + '\t'
            print output

    def _check_rec(self, i, j):
        # 检查某个方格是否反转
        result = 0
        if i > 0:
            result += self._matrix[i-1][j]
        if i < self.n-1:
            result += self._matrix[i+1][j]
        if j > 0:
            result += self._matrix[i][j-1]
        if j < self.n-1:
            result += self._matrix[i][j+1]
        result += self._matrix[i][j]

        return result % 2 == 1

    def _check_result(self):
        # 检查最后得出的矩阵是否全部反转
        for i in range(self.n):
            for j in range(self.n):
                assert self._matrix[i][j] >= 0
                if not self._check_rec(i, j):
                    return False
        return True

    def _define_rec_val(self, i, j):
        # 确定(i, j)方格的值
        # return 0: 值是否是猜测
        # return 1: 值
        guess = True
        
        above_val = -1
        if i > 0:
            above_val = 0
            if i > 1:
                above_val += self._matrix[i-2][j]
            if j > 0:
                above_val += self._matrix[i-1][j-1]
            if j < self.n-1:
                above_val += self._matrix[i-1][j+1]
            above_val += self._matrix[i-1][j]

        if above_val != -1:
            guess = False
            result = 0 if above_val%2==1 else 1
            return guess, result

        return guess, 0

    def _clear(self, i, j):
        # 将(i, j)之后的方块重置-1值
        for k in range(self.n):
            for l in range(self.n):
                if k>i or (k==i and l>=j):
                    self._matrix[k][l] = -1           

    def _run(self, i, j, start=True):
        # 主运行函数
        if not start: self._clear(i, j)
        else:
            self._guess_list.append((i, j))
        
        guess = 0 if start else 1
        self._matrix[i][j] = guess
        
        for k in range(self.n):
            for l in range(self.n):
                if k > i or (k==i and l>j):
                    temp = self._define_rec_val(k, l)
                    if temp[0] == True:
                        # 如果为猜测
                        self._matrix[k][l] = temp[1]
                        self._guess_list.append((k, l)) #添加至猜测列表
                    else:
                        self._matrix[k][l] = temp[1]

        if self._check_result():
            print 'Result: '
            self.display()
        else:
            if len(self._guess_list) > 0:
                self._run(*(self._guess_list.pop()), start=False)
        
        
    def __call__(self):
        self._run(0, 0)


if __name__ == '__main__':
    import sys
    n = 5
    if len(sys.argv) > 1:
        n = int(sys.argv[1])
    m = Matrix(n)
    m()

在命令行中运行脚本（可以指定每行方块数，如运行“python ***.py 5”），当n=5时，结果如下：

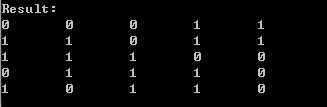
按照这个策略点击，可以得出正确结果。当然，如果想得出全部结果，修改代码也很容易。