波特词干算法
在英语中,一个单词常常是另一个单词的“变种”,如:happy=>happiness,这里happy叫做happiness的词干(stem)。在信息检索系统中,我们常常做的一件事,就是在Term规范化过程中,提取词干(stemming),即除去英文单词分词变换形式的结尾。
应用最为广泛的、中等复杂程度的、基于后缀剥离的词干提取算法是波特词干算法,也叫波特词干器(Porter Stemmer)。详见官方网站。比较热门的检索系统包括Lucene、Whoosh等中的词干过滤器就是采用的波特词干算法。
简单说一下历史:
马丁.波特博士(Dr. Martin Porter)于1979年,在英国剑桥大学,计算机实验室,发明了波特词干算法。
波特词干算法当时是作为一个大型IR项目的一部分被提出的。它的原始论文为:
C.J. van Rijsbergen, S.E. Robertson and M.F. Porter, 1980. New models in probabilistic information retrieval. London: British Library. (British Library Research and Development Report, no. 5587).
最初的波特词干提取算法是使用BCPL语言编写的。作者在其网站上公布了各种语言的实现版本,其中C语言的版本是作者编写的最权威的版本。
波特词干器适用于涉及到提取词干的IR研究工作,其实验结果是可重复的,言外之意是说,波特词干器的输出结果是确定性的,不是随机的。(还有基于随机的高级词干提取算法,虽然会更准确,但同时也更加复杂)。
词干提取算法无法达到100%的准确程度,因为语言单词本身的变化存在着许多例外的情况,无法概括到一般的规则中。使用词干提取算法能够帮助提高IR的性能。
波特词干算法的官方网站上,有各个语言的实现版本(其实都是C标准的各个翻译形式)。各位要应用到实际生产中可以直接下载对应的版本。本文将会分析Java语言的源码。在今后的文章中,再介绍使用Python特性优化过的版本。(Python原版几乎就是C语言版本的翻译,这也就意味着不能充分利用Python的语言特性。)
超能饮料问题
今天讨论超能饮料的问题。这里是题目的来源。这个超能饮料的题目,颇有些炒作的嫌疑。据说这道题是程序员百万年薪招聘的题目之一。今天也是无意中从同学那里知道,这里就简单给出思路,然后给出Python语言的实现版本。
这里简单说一下超能饮料问题的大意。现在,已知有若干种原料,它们以C开头,比如:C1、C2.......一种原料转化为另一种原料需要使用定制的机器,而这也是成本主要来源(原料成本不计)。机器标记以M开头,如:M1、M2......
现在我们有一系列的输入(命令行参数形式,给出文件名,以文件形式读入),文件的每一行都代表特定的设备型号。每一行的格式如下:
<machine name> <orig compound> <new compound> <price>(分别对应的中文意思是设备名称、源化合物、新化合物、价格)
输入文件示例:
M1 C1 C2 277317
M2 C2 C1 26247
M3 C1 C3 478726
M4 C3 C1 930382
M5 C2 C3 370287
M6 C3 C2 112344
题目的要求是,求无论能买到那种原料,都保证能生产出其他原料,并且保证花费的代价最小。
要求返回值的格式为:第一行,最优总价格。第二行,机器列表(去掉开头M),比如上例的输出示例:
617317
2 3 6
读完这条题目,我们可以发现,这题目其实是一条典型的图论题。对于某一个状态Ci,我们可以通过Mk转移至Cj,权重为Wm。于是,根据题意,我们实际上要求的是这样一条或者多条环路,使得它们包含所有的原料,并且,环路上所有的权重和最小。
在此基础上,我们必须满足两点。
- 这条环路必须包含所有的原料。如果不能满足包含全部原料,就不能保证“无论能买到哪种原料,都保证能生产出其他原料”的条件。
- 对于重复出现的状态转移,只需计算一遍。
综上所述,问题要解决的在已知图中求一条或多条环路,并且使这些环路中包含所有原料。
动态规划求编辑距离
这两天在写一个简单的单词拼写检查器(Spell checker),本来求编辑距离只是其中的一个子问题,现在把它罗列出来,是因为鉴于看到一些书,把本来不是很难的问题讲得很复杂,而且不知道是不是一些作者,为了显得自己水平之高,几乎没有任何的推导,只有一堆结果罗列。当然这些都是题外话了,但是,书者,传道授业解惑也,若是使读者迷惑不能自拔,不知是读者愚钝,还是书之不书。
现在我们开始切入正题。先来说说什么是编辑距离,编辑距离是一种字符串之间相似程度的计算方法。按照Damerau给出的定义,即两个字符串之间的编辑距离等于使一个字符串变成另外一个字符串而进行的(1)插入、(2)删除、(3)替换或(4)相邻字符交换位置而进行操作的最少次数。用ed来表示编辑距离。
比如:ed("recoginze", "recognize") == 1(需要交换两个相邻字符"i"和"n"的位置)
ed("sailn", "failing") == 3(需要将"s"换成"f",在字母"l"后边插入"i","n"后面插入"g")。
有的时候,变换并不唯一,重要的是要求出这一些变换路径中最短的数量。
关于编辑距离的求法,普遍的采用的是动态规划方法。但是,目前网上的资料中提及的编辑路径并不准确,缺少了第(4)步的处理。详细的同学们可以查阅这两篇文章——【串和序列处理 2】字符串编辑距离算法(Java)和动态规划求编辑距离——算法解题报告(C++)。
下面给出维基上对动态规划的定义:
动态规划是一种在数学和计算机科学中使用的,用于求解包含重叠子问题的最优化问题的方法。其基本思想是,将原问题分解为相似的子问题,在求解的过程中通过子问题的解求出原问题的解。
其实就是把一个复杂的最优解问题分解成一系列较为简单的最优解问题,再将较为简单的最优解问题一步步分解,直到能够一眼看出为止。
我们拿"sailn"和"failing"这两个字符串作例子。首先我们定义这样一个函数——edit(i, j),它表示字符串1的长度为i的子串到字符串2的长度为j的子串的编辑距离。
首先我们作出初始化edit(0, j) = j(字符串1子串长度为0,字符串2子串有多少个字符,就作多少次增加操作;于是同理,edit(i, 0) = i。)
这里,我们要注意到对于操作(4),即交换相邻字符串的操作,我们要把某个字符通过这个操作到另一个位置上,我们最多只能执行一次操作,即只能移动到邻位上。原因是什么呢?这是因为,移动两次的话,就没有优势了,它的操作等于两次替换操作的操作数。大于2次的时候,移动操作会更差。所以,我们要进行操作(4),最多只发生一次操作。
我们可以得出这样一段动态规划公式:
- 如果i == 0 且 j == 0,edit(i, j) = 0
- 如果i == 0 且 j > 0,edit(i, j) = j
- 如果i > 0 且j == 0,edit(i, j) = i(2、3点之前已经陈述)
- 如果0 < i ≤ 1 且 0 < j ≤ 1 ,edit(i, j) == min{ edit(i-1, j) + 1, edit(i, j-1) + 1, edit(i-1, j-1) + f(i, j) },这里当字符串1的第i个字符不等于字符串2的第j个字符时,f(i, j) = 1;否则,f(i, j) = 0。
- 如果i > 1且 j > 1时,这个时候可能出现操作(4),由之前的推导,我们只能交换一次,否则就没有意义。这个时候在比较最小值中可能加入edit(i-2, j-2) +1,什么时候加入呢?假设i-2长度的字符串1子串和j-2长度的字符串2子串已经得出最优解,这个时候如果s1[i-1] == s2[j] 并且s1[i] == s2[j-1],这时就在比较值中加入edit(i-2, j-2) + 1(这个1是交换一次的操作)
关于阶乘的一些讨论
我们今天要讨论的问题大意是:给定一个数n,判断是否存在一个数m,使得:n == ∑i!(这里共m个不同整数)。(n≤1000000)
说白了其实就是:给定一个数n,看看这个数能不能表示成从m个不同整数阶乘的和。
刚拿到题目可能没有思路。仔细考虑可以注意到,n的最大值为1000000,小于32位机器上的int型的最大值(2^31-1),最先可能想到的是枚举法,由于10!>1000000,所以可能出现的0-9这几个数,每个数都有出现或者不出现两种情况,如果枚举将会有2^10共1024种情况,这个数量也不小。这就意味着需要换个思路来考虑。
注意到,对于一个整数k(k>1),0! + 1! + ... + (k-1)! < k!(左边 < k * (k-1)! == k!),因此,我们可以得出结论,对于一个数n,假设一个数j,使得j! ≤ n 且 (j+1)! > n,那么n分解成阶乘和的数中必定包含j!,用反证法证明,假设不包含,由之前的结论,小于j的所有数的阶乘和都小于j!,当然也必小于n。因此,当n = n - j!后,再判断n是否等于新的j!,等于证明分解成功;否则就减去新的j!,并循环判断。
于是,我们很容易得出以下代码。
public final static int count = 10;
public static int[] Facs(){
int temp = 1;
int[] facs = new int[count];
for(int i=0; i<count; i++){
if(i != 0)
temp = temp * i;
facs[i] = temp;
}
return facs;
}
public static boolean facsSum(int n){
int rest = n;
int current = count - 1;
int[] facs = Facs();
while(rest >= 0 && current >= 0){
if(rest >= facs[current]){
rest -= facs[current];
}
current--;
}
if(rest == 0)
return true;
return false;
}
这里有个技巧,在上面的代码中,Facs函数把0到9的阶乘储存在一个数组当中。这里有的同学可能会这么写代码。
private static int factorials(int n){
if(n<=1)
return 1;
return factorials(n-1)*n;
}
private static int[] Facs(){
int[] retFacs = new int[count];
for(int i=0; i<count; i++){
retFacs[i] = factorials(i);
}
return retFacs;
}
注意到差别没有,其实我们上一次用到的阶乘存放在临时数中,下轮就可以直接拿来使用。第二种方法更直观,但是重复的运算、加上递归的使用,使代码的效率低了许多。
因此,大家可以试试只用一个循环来计算1到100阶乘的和。
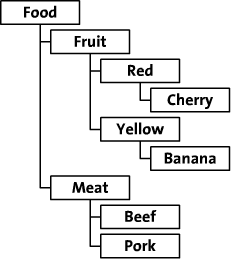
在数据库中存储层级结构
本文参考自这篇文章。文章是2003年的,但是现在来看仍然有着实际意义。
层级结构,也叫树形结构。在实际应用中,你经常需要保存层级结构到数据库中。比如说:你的网站上的目录。不过,除非使用类XML的数据库,通用的关系数据库很难做到这点。
对于树形数据的存储有很多种方案。主要的方法有两种:邻接表模型,以及修改过的前序遍历算法。本文将会讨论这两种方法的实现。这里的例子沿用参考文章中的例子,原文使用的PHP,这里将会用Java替代。(本例使用Mysql数据库,Java如何连接Mysql,见备注一。)文中使用虚拟的在线食品商店作例子。这个食品商店通过类别、颜色以及种类来来组织它的食品。如图所示: