残阳似血的博客

今天讨论超能饮料的问题。这里是题目的来源。这个超能饮料的题目，颇有些炒作的嫌疑。据说这道题是程序员百万年薪招聘的题目之一。今天也是无意中从同学那里知道，这里就简单给出思路，然后给出Python语言的实现版本。

这里简单说一下超能饮料问题的大意。现在，已知有若干种原料，它们以C开头，比如：C1、C2.......一种原料转化为另一种原料需要使用定制的机器，而这也是成本主要来源（原料成本不计）。机器标记以M开头，如：M1、M2......

现在我们有一系列的输入（命令行参数形式，给出文件名，以文件形式读入），文件的每一行都代表特定的设备型号。每一行的格式如下：

<machine name>  <orig compound>  <new compound>  <price>（分别对应的中文意思是设备名称、源化合物、新化合物、价格）

输入文件示例：

M1  C1  C2  277317
M2  C2  C1  26247
M3  C1  C3  478726
M4  C3  C1  930382
M5  C2  C3  370287
M6  C3  C2  112344

题目的要求是，求无论能买到那种原料，都保证能生产出其他原料，并且保证花费的代价最小。

要求返回值的格式为：第一行，最优总价格。第二行，机器列表（去掉开头M），比如上例的输出示例：

617317
2 3 6

读完这条题目，我们可以发现，这题目其实是一条典型的图论题。对于某一个状态Ci，我们可以通过Mk转移至Cj，权重为Wm。于是，根据题意，我们实际上要求的是这样一条或者多条环路，使得它们包含所有的原料，并且，环路上所有的权重和最小。

在此基础上，我们必须满足两点。

1. 这条环路必须包含所有的原料。如果不能满足包含全部原料，就不能保证“无论能买到哪种原料，都保证能生产出其他原料”的条件。
2. 对于重复出现的状态转移，只需计算一遍。

综上所述，问题要解决的在已知图中求一条或多条环路，并且使这些环路中包含所有原料。

深夜，安静得听的见心跳。本已躺下，不知是什么，让心中埋藏的各种三月的情感奔涌而来；不知是什么，让眼泪落湿了枕巾。可以说我矫作，我已不在乎。脑海中的一切，已变成一个幻灯片，一幕幕的画面，闪过的时候，开始总是灰心一笑，可紧接着袭来的是无尽的难过，这种滋味，可能只有三月的们才能明白。

那末，就从三月开始说起。

一

高中时我们一个班，那时候大家的生活似乎没有过多的交集。贝贝和刁刁坐在第一排，丫头在她们之后坐第二排，她们仨是一拨。那个时候，男女生之间的关系极其保守，女生占前两排，男生之后坐起。A杜、高夫坐在一起，他们之后是仓木娘。他们是一拨，同时他们也是我们当中最早和三个女生（姑且这么认为，是么？:) ）有联系的。我和老钱坐一起，之后是进。我们仨是一拨，朱建单独坐其他地方。

当时，我们是班上成绩不错的，所以，这可能是后来把我们聚合一起的原因之一。

在那个时候，学习是件极其艰苦的事情，披星戴月的大家，没有多余的时间交流。那时的印象只是：贝贝的嗓门挺大，刁刁的资料老是被班主任拿来讲。丫头是焦点人物，当时学校里有很多闷骚的男生们跑来看她（校花有力人选），同时她成绩又好得很，老师前的红人（那时，我大多考试会被丫头击败）。A杜成绩不错，而且和他几乎从幼儿园就开始同学，太熟了。高夫是老师前的红人，数理化很不错，重要的是有两颗吸血鬼般的虎牙，一张稚气的脸，一付小不点的身材（现在一点也不小）。仓木娘是数学课代表，数理化三门极其好，可是语文英语很糟糕。哦，对了，仓木娘在我们的方言中是“丈母娘”的意思。名字的来源是，当时我们的语文老师韩建，叫他名字时候，我们总以为叫丈母娘，于是就有了这个称号。朱建呢，为人低调，长得很帅，成绩当然也很不错。最重要的是，直到本科毕业，他那唏嘘的胡喳子，忧郁的眼神，嘚啵嘚啵的皮鞋声，一成不变。

高中时我们中熟得很的自然就是老钱和进了。老钱，那个时候常常说出巨猥琐的话，而且还经常招我打（这点，我想起竟然有些过意不去的感觉）。进坐在我后面，那时，我们都是数学狂热爱好者，常互出题目考对方，然后一起考老师。那时候，他冷不丁得用国际奥赛的题目难我，我呢，则是用自己编的“杀手锏”题目来考他（当然，时常出错）。我们那时候喜欢听周杰伦的歌，他那时喜欢《东风破》歌词，一起背。那时候，我每到早读晚读，都不读书，在那里大声唱歌，还招呼周围的人听我演唱会。上课或自习时，我、进、钱几个常偷偷讲话，交换小说漫画杂志。高中的时间艰苦但却无忧无虑。我是个爱讲冷笑话的人，直到现在，每次也只有进都能听懂。

“三月广场”这个称号据说也就是那个时候贝贝和刁刁俩人拍脑门子决定的。大概是这样：“你不觉得三月这个名字很酷么？”“很酷，要是再加个广场会更酷。”

毕业了，我、A杜、刁刁和朱建四人考上了东南大学（作为江苏人，我很为东大不平，不错的大学，声名却着实不响，在江苏也很难考，可是很多人甚至不知东大在南京）。高夫去了南京大学。进考上武汉大学，贝贝上了武汉科技大学。老钱去了中国矿业大学（徐州）。丫头和仓木娘去了上海，丫头去了上海外国语大学，仓木娘去了上海海事大学。

虽然那是大家已经天各一方，但着实算不上远。

在平常的代码中，我们常常需要与时间打交道。在Python中，与时间处理有关的模块就包括：time，datetime以及calendar。这篇文章，主要讲解time模块。

在开始之前，首先要说明这几点：

1. 在Python中，通常有这几种方式来表示时间：1）时间戳 2）格式化的时间字符串 3）元组（struct_time）共九个元素。由于Python的time模块实现主要调用C库，所以各个平台可能有所不同。
2. UTC（Coordinated Universal Time，世界协调时）亦即格林威治天文时间，世界标准时间。在中国为UTC+8。DST（Daylight Saving Time）即夏令时。
3. 时间戳（timestamp）的方式：通常来说，时间戳表示的是从1970年1月1日00:00:00开始按秒计算的偏移量。我们运行“type(time.time())”，返回的是float类型。返回时间戳方式的函数主要有time()，clock()等。
4. 元组（struct_time）方式：struct_time元组共有9个元素，返回struct_time的函数主要有gmtime()，localtime()，strptime()。下面列出这种方式元组中的几个元素：

Django mptt是个Django第三方组件，目标是使Django项目能在数据库中存储层级数据（树形数据）。它主要实现了修改过的前序遍历算法，如果你对原理还不是很了解，可以看我的这篇文章。当然，使用mptt时，原理是可以不用了解的，因为具体的实现细节都已经隐藏。不过，如果项目不是使用的Django，可以参考具体的实现原理。

在整篇文章中，我们将会拿《在数据库中存储层级结构》中的例子作为本文的例子。我们打算在数据库中存储这张图中的数据：

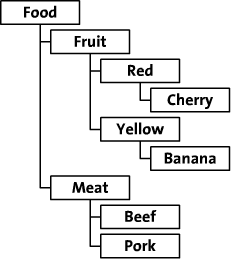
在介绍mptt之前，如果你的需求仅仅是像这样显示以上数据：

Food
    
 
        
Fruit
        
 
            
Red
            
 
               
Cherry
 
            
 
            
 
            
Yellow
            
 
               
Banana
 
            
 
            
 
        
 
        
 
        
Meat
        
 
            
Beef
 
            
Pork
 
        
 
        
 
    
 
 

mptt就显得大材小用了，因为Django已经有内置模板过滤器来完成这个工作：unordered_list（官方文档）。如果你的需求不只这么简单，那就跳过这一段。不过这里还是要讲解一下unordered_list的做法。我们就来实现以上的结果。

这两天在写一个简单的单词拼写检查器（Spell checker），本来求编辑距离只是其中的一个子问题，现在把它罗列出来，是因为鉴于看到一些书，把本来不是很难的问题讲得很复杂，而且不知道是不是一些作者，为了显得自己水平之高，几乎没有任何的推导，只有一堆结果罗列。当然这些都是题外话了，但是，书者，传道授业解惑也，若是使读者迷惑不能自拔，不知是读者愚钝，还是书之不书。

现在我们开始切入正题。先来说说什么是编辑距离，编辑距离是一种字符串之间相似程度的计算方法。按照Damerau给出的定义，即两个字符串之间的编辑距离等于使一个字符串变成另外一个字符串而进行的（1）插入、（2）删除、（3）替换或（4）相邻字符交换位置而进行操作的最少次数。用ed来表示编辑距离。

比如：ed("recoginze", "recognize") == 1（需要交换两个相邻字符"i"和"n"的位置）

ed("sailn", "failing") == 3（需要将"s"换成"f"，在字母"l"后边插入"i"，"n"后面插入"g"）。

有的时候，变换并不唯一，重要的是要求出这一些变换路径中最短的数量。

关于编辑距离的求法，普遍的采用的是动态规划方法。但是，目前网上的资料中提及的编辑路径并不准确，缺少了第（4）步的处理。详细的同学们可以查阅这两篇文章——【串和序列处理 2】字符串编辑距离算法（Java）和动态规划求编辑距离——算法解题报告（C++）。

下面给出维基上对动态规划的定义：

动态规划是一种在数学和计算机科学中使用的，用于求解包含重叠子问题的最优化问题的方法。其基本思想是，将原问题分解为相似的子问题，在求解的过程中通过子问题的解求出原问题的解。

其实就是把一个复杂的最优解问题分解成一系列较为简单的最优解问题，再将较为简单的最优解问题一步步分解，直到能够一眼看出为止。

我们拿"sailn"和"failing"这两个字符串作例子。首先我们定义这样一个函数——edit(i, j)，它表示字符串1的长度为i的子串到字符串2的长度为j的子串的编辑距离。

首先我们作出初始化edit(0, j) = j（字符串1子串长度为0，字符串2子串有多少个字符，就作多少次增加操作；于是同理，edit(i, 0) = i。）

这里，我们要注意到对于操作（4），即交换相邻字符串的操作，我们要把某个字符通过这个操作到另一个位置上，我们最多只能执行一次操作，即只能移动到邻位上。原因是什么呢？这是因为，移动两次的话，就没有优势了，它的操作等于两次替换操作的操作数。大于2次的时候，移动操作会更差。所以，我们要进行操作（4），最多只发生一次操作。

我们可以得出这样一段动态规划公式：

1. 如果i == 0 且 j == 0，edit(i, j) = 0
2. 如果i == 0 且 j > 0，edit(i, j) = j
3. 如果i > 0 且j == 0，edit(i, j) = i（2、3点之前已经陈述）
4. 如果0 < i ≤ 1  且 0 < j ≤ 1 ，edit(i, j) == min{ edit(i-1, j) + 1, edit(i, j-1) + 1, edit(i-1, j-1) + f(i, j) }，这里当字符串1的第i个字符不等于字符串2的第j个字符时，f(i, j) = 1；否则，f(i, j) = 0。
5. 如果i > 1且 j > 1时，这个时候可能出现操作（4），由之前的推导，我们只能交换一次，否则就没有意义。这个时候在比较最小值中可能加入edit(i-2, j-2) +1，什么时候加入呢？假设i-2长度的字符串1子串和j-2长度的字符串2子串已经得出最优解，这个时候如果s1[i-1] == s2[j] 并且s1[i] == s2[j-1]，这时就在比较值中加入edit(i-2, j-2) + 1（这个1是交换一次的操作）